Numerical Solution to Navier-Stokes
Simple numerical solution to Navier-Stokes using FreeFEM++
The Problem
This is the final post in the series of simulation using Freefem++, where I sum up how to solve Navier-Stokes equations numerically. As mentioned in previous post, I have very limited background in physics, so I cannot fully understand why and how physicist came up with the Navier-Stokes equations for incompressible fluid. Therefore this blog is presented in a mathematical perspective (which basically mean that I agree with everything the physicists said and only do the math and the coding). Now let me formally restate the famous Navier-Stokes equations: \(\begin{align} \rho \left(\frac{\partial u}{\partial t} + (u . \nabla) u \right) - \mu \Delta u + \nabla v & = \rho f \tag{1} \\ \text{div} & = 0 \tag{2} \end{align}\)
where \(u(x, t)\) is velocity of the stream at position \(x\) (\(x \in \mathcal{R}^2\) or \(x \in \mathcal{R}^3\)) at time \(t\), and \(p(x, t)\) is the pressure of the fluid. The Navier-Stokes asks to find \(u\) and $v$ which satisfies (1) and (2) with given fluid property \(\rho\) (density) , \(\mu\) (viscosity) and external force applied on each volume unit \(f\).
Note that, since \(u\) is vector value function, (1) is actually short-handed for 2 equations in \(\mathcal{R}^2\) (or 3 equations in \(\mathcal{R}^3\)).
Numerical solution
The following program describe how water flow in a pipe (as shown in the figure) given that at one end the velocity of the water is kept at constant, there is some round-shaped obstacle within the pipe and the stream at the other end is allowed to move freely. The mysterious epsilon in the weak equations is require for the stability.
int n=100;
real T=1;
real dt=0.01;
int count=0;
border s1(t=5,20){x=t;y=0;label=1;};
border s2(t=0,3){x=20;y=t;label=2;};
border s3(t=20,0){x=t;y=3;label=1;};
border s4(t=3,1){x=0;y=t;label=3;};
border s5(t=0,5){x=t;y=1;label=1;};
border s6(t=1,0){x=5;y=t;label=1;};
border c(t=0, 2*pi){x = 10 + 0.25*cos(t); y = 1.5 + 0.25*sin(t);}
mesh Th= buildmesh (s1(n)+s2(n)+s3(n)+s4(n)+s5(n)+s6(n)+c(-n));
plot(Th);
fespace Uh(Th,P1b);
Uh u1,u2,v1,v2,u1old=0,u2old=0,
f1,f2;
fespace Ph(Th,P1);
Ph p, q;
real epsilon=1e-10;
real mu=1e-5;
f1=0;
f2=0;
real alpha =1/dt;
solve stokes([u1,u2,p],[v1,v2,q])=
int2d(Th)((u1*v1+u2*v2)*alpha)
+int2d(Th)(mu*(dx(u1)*dx(v1)+dy(u1)*dy(v1)+dx(u2)*dx(v2)+dy(u2)*dy(v2)))
-int2d(Th)(p*(dx(v1)+dy(v2)))
-int2d(Th)(f1*v1+f2*v2)
+int2d(Th)(q*(dx(u1)+dy(u2))-epsilon*p*q)
+int2d(Th)(-alpha*convect([u1old,u2old],-dt,u1old)*v1
-alpha*convect([u1old,u2old],-dt,u2old)*v2)
+on(1,u1=0,u2=0) +on(3,u1=0.667,u2=0) + on(c, u1=0, u2=0);
for (int i=0;i<T/dt;i++){
count++;
stokes;
plot([u1,u2],p, ps="ns_" + count +".jpg");
u1old=u1;
u2old=u2;
}
Ph psi,phi;
solve streamlines(psi,phi) =
int2d(Th)(dx(psi)*dx(phi) +dy(psi)*dy(phi))
+int2d(Th)(-phi*(dy(u1)-dx(u2)))
+on(1,2,3,4,psi=0);
plot(psi, ps="streamline.jpg");
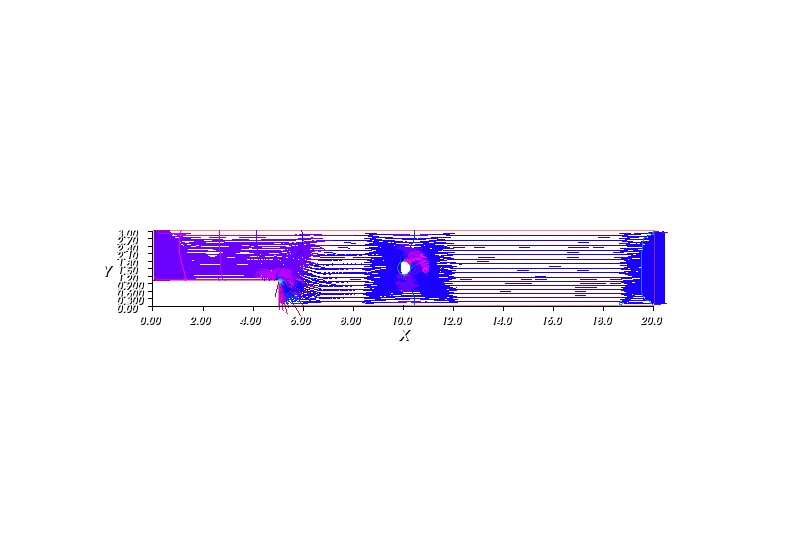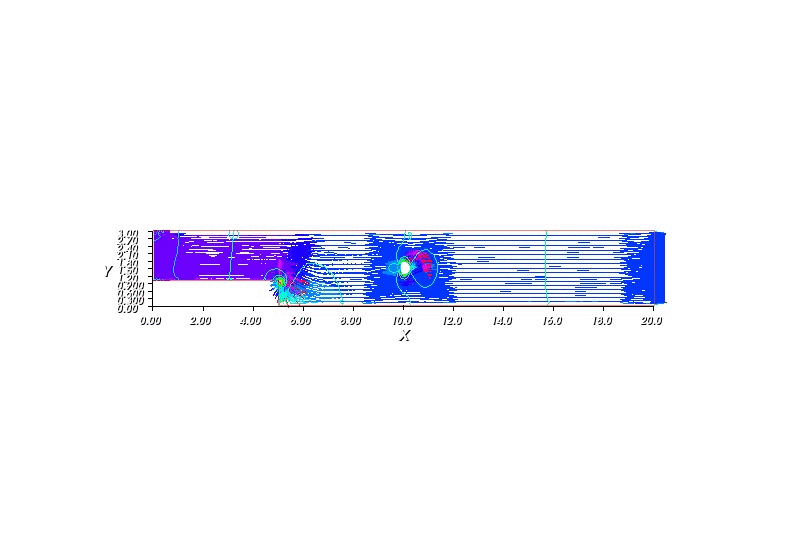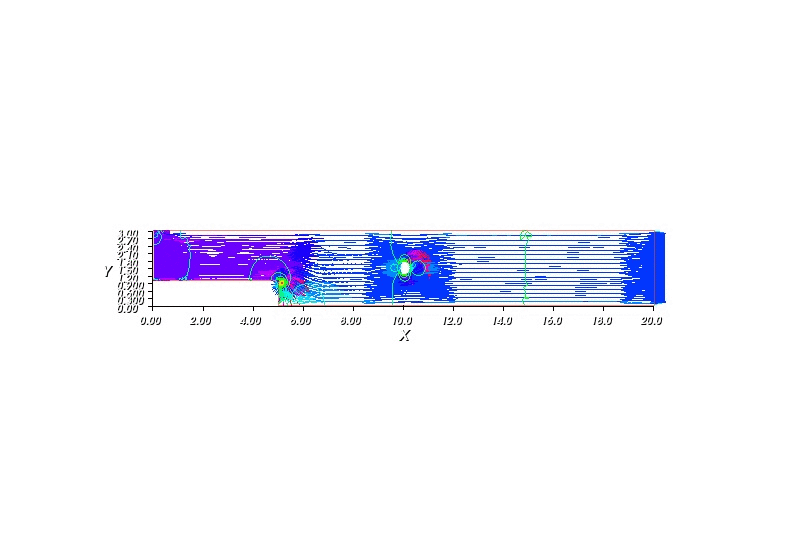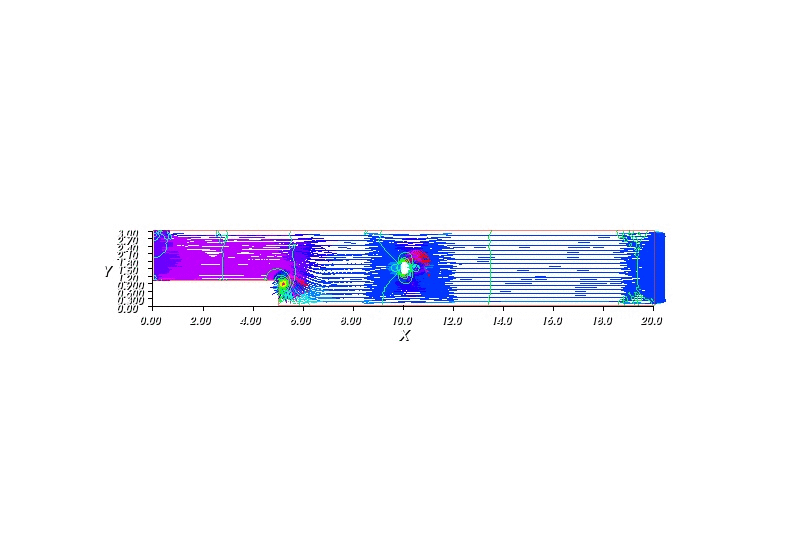
Another way to view the flow is through streamlines. A streamline is a curve whose point has velocity vector tangent to it. Mathematically, streamlines can be define as a function \(\psi\) satifsies: \(u = \left(\frac{\psi}{y}, -\frac{\psi}{x} \right)^T\)
